经典图论问题。一个二分图 G 的最小顶点覆盖的顶点数量与其最大匹配中的边数量相等。网络上其实有很多该定理的证明,本文尝试用一种更为直观的图文结合证明方法解释这个定理的正确性。
相关概念
基础概念:
- 二分图:如果一个图 G = <V, E> 中的顶点集合 V 可以被划分成不相交的两部分,并且 G 中所有的边的两个顶点都分别属于这两个部分,那么称 G 为二分图(或者二部图)。
- 顶点覆盖:G = <V, E> ,如果 V 的一个子集 V0,使得所有边至少有一个点在 V0 中,则称 V0 为 G 的一个顶点覆盖。
- 最小顶点覆盖:含有最少顶点数的一个顶点覆盖。
- 匹配:G = <V, E> ,如果 E 的一个子集 E0,其中任意两条属于 E0 的边都没有公共顶点,则称 E0 是 G 的一个匹配。
- 最大匹配:含有最多边数的一个匹配。
辅助概念:
- 匹配边:对于图 G 和对于 G 的一个匹配 E0 而言,E0中的边称为匹配边。
-
未匹配边:对于图 G = <V, E>,和对于 G 的一个匹配 E0 而言,E - E0 中的边称为未匹配边。
-
未匹配的点:对于图 G 和对于 G 的一个匹配 E0 而言,如果顶点 p 不在 E0 的任何一条边中,则称 p 为未分配的点。
- 增广路(argumenting path):对于二分图 G 和对于 G 的一个匹配 E0 而言,若存在一条路径<e0, e1, …, ek>,起始点和终点均为“未分配的点”,并且“未匹配边”和“匹配边”交替出现(开始和结尾均为“未匹配边”),那么称这条路径为增广路。
概念的例子
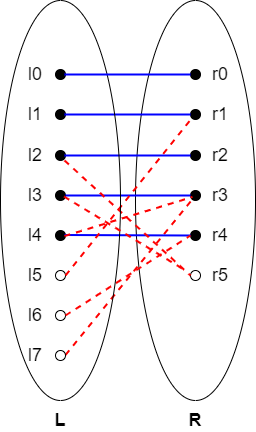
- 图 G = <V, E>,其中 V 就是黑色的点,E 就是蓝色实线和红色虚线的并集,那么显然 G 可以被分为 L 和 R 两部分,所以 G 是一个二分图。
- 蓝线集合是 G 的一个匹配,每条蓝线是一个匹配边。
- 红线是未匹配边。
- 空心的点都是未匹配的点。
- l6 -> r4 -> l4 -> r3 -> l3 -> r5 是一条增广路,l7 -> r3 -> l3 -> r5 也是一条增广路。
证明
引理1:最大匹配中不存在增广路。
容易发现,增广路中未匹配边比匹配边数量多1。
反证法:假设某个最大匹配中存在一条增广路。
将增广路中的匹配边与未匹配边交换可以产生一个新的匹配,因为去掉增广路中所有匹配边,那么图中没有任何一条边包含增广路中的点,又由于未匹配边是交替出现的,不共用顶点,所以将未匹配边加入后仍然满足匹配的定义。
那么产生的新的匹配中边的数量比原先多1,与最大匹配矛盾。
引理2:最小顶点覆盖的顶点数量 ≥ 最大匹配中的边数
由于最大匹配是一个匹配,边之间没有公共点,那么每条边中至少有一个点属于最小顶点覆盖,因而得证。
通过一个最大匹配构造顶点覆盖
定义(半条增广路):如果有一条有向路径,开始于一个“未匹配的点”和一条“未匹配边”,之后交替出现“匹配边”和“未匹配边”并且以“未匹配边”结束,那么称这条路径为“半条增广路”。
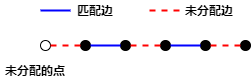
将一个最大匹配中,所有“半条增广路”的终点标记为“绿色”。那么对于所有的“未匹配边”来说,如果该边的两个顶点均不为绿色,有以下几种情况:
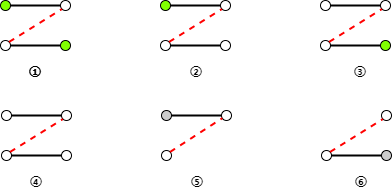
- ①:不可能,如果右下角已经被标记绿色,说明有一条以右下角顶点为终点的“半条增广路”,那么加上下面的“匹配边”与这条“未匹配边”之后,构成了新的“半条增广路”,与我们假设的所有终点被标记矛盾。
- ②:不可能,与①类似,左下角的顶点应当也被标记为绿色。
- ③:不可能,与①②类似,右上角的点应当被标记为绿色。
- ④:可能!与这条“未匹配边”相关的两条“匹配边”的四个顶点均为被标记为绿色。
- ⑤:不可能:左下角为“未匹配的点”,那么这条“未匹配边”可以单独构成“半条增广路”,右上角应为绿色。
- ⑥:不可能:与⑤类似。
那么如果我们将所有两个顶点都未被标记的“匹配边”的左侧顶点标记为绿色,所有的未匹配边与匹配边将均被“绿色顶点”覆盖。因而“绿色顶点集合”是一个顶点覆盖。因而有推论,所有匹配边上至少有一个绿色顶点。
下面证明所有“匹配边”上没有两个绿色顶点(两个顶点不均为绿色)。
如果某条“匹配边”的两个顶点均为绿色,那么存在两条“半条增广路”以这两个顶点为终点。那么容易发现这两条“半条增广路”加上这条“匹配边”构成了一条“增广路”(如下图所示)。而由引理1知,最大匹配中不存在增广路,矛盾。因而每条“匹配边”至多有一个点为绿色。
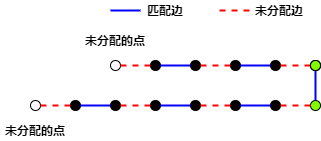
因而,该最大匹配中,每条“匹配边”均恰好有一个点被标记为“绿色”,且所有“绿色顶点”构成一个“顶点覆盖”,基数等于最大匹配的边数。又因为引理2得知,该“顶点覆盖”是“最小顶点覆盖”。所以原命题得证。